3DアニメーションをCSS化する方法

1 . 概要
ウェブサイトに3Dモデルを実装する場合、CSSで3Dモデルを作ると大変だと思います。
今回Blenderの3DモデルからHTMLとCSSコードに変換する方法を紹介します。
2 . CSS変換プログラム用意
2.1. 3次元の中に4ポイント以上なら同じ平面に属しない可能性があるため、3Dモデルを三角形に分割します。(Blenderは自動的に分割できる機能があります。)
2.2. 各平面をz=C(C:定数)平面になるように回転させると平面の法線からベクターベクター(0,0,1)に回転マトリックスが抽出できます。このマトリックスをRと呼びます。
2.3. ステップ2.2で3Dモデルが回転されたことにより平面座標も変更されているため、再計算する必要があります。この平面のポイントのzはCとなります。
2.4. 再計算後、ポイントの中心が(0,0,0)になるように平面を移動させます。 中心の座標はx=(xmin + xmax) / 2。移動するマトリックスをTと呼びます。
2.5. ステップ2.4で移動した上で、平面の3ポイントはz=0平面に属すようになります。z=0平面で<div> タグを平面の周囲に沿ってカットします。この処理と平面の色はCSSファイルで定義します。
2.6. CSSでは 「T」ベクターに沿って逆移動処理を行い、「R」ベクターに沿って逆回転を行い、元の平面に復元できます。
2.7. ステップ2.2~2.6の計算量が多いため、手動で計算するのは難しいです。そのためCSS変換プログラムとしてPythonスクリプトを利用して計算させることにします。これを利用すると簡単にBlender 3DモデルファイルからCSSファイルに変換できます。もし試してみたい場合は以下のPythonスクリプトをコピーし、ファイル名は「convert.py」としてください。
# convert.py
import numpy as np
import sys
def load_data(obj_file):
# load point positions
f = open(obj_file)
s = f.read()
f.close()
elements = s.split('\n')
elements = list(filter(lambda element: element.startswith("o ") or element.startswith("v ") or element.startswith("f ") or element.startswith("vn ") ,elements))
objs = {}
vertices = []
vertex_norms = []
current_obj = []
for element in elements:
if element.startswith("o "):
current_obj = []
parts = element.split(" ")
parts = parts[1].split("_")
objs[parts[0]] = current_obj
elif element.startswith("v "):
parts = element.split(" ")
vertices.append(np.float32([float(parts[1]),float(parts[2]),float(parts[3])]))
elif element.startswith("vn "):
parts = element.split(" ")
vertex_norms.append(np.float32([float(parts[1]),float(parts[2]),float(parts[3])]))
elif element.startswith("f "):
parts = element.split(" ")[1:]
norm_id = int(parts[0].split("/")[2])
parts = [int(x.split("/")[0])-1 for x in parts]
face = np.float32([vertices[i] for i in parts])
face = face[:, [0,2,1]]
norm = vertex_norms[norm_id-1]
norm = norm[[0,2,1]]
current_obj.append({"face": face, "norm": norm})
return objs
def make_rotation_matx(angle):
return np.float32([
[1, 0, 0],
[0, np.cos(angle), -np.sin(angle)],
[0, np.sin(angle), np.cos(angle)]
])
def make_rotation_maty(angle):
return np.float32([
[np.cos(angle), 0, np.sin(angle)],
[0, 1, 0],
[-np.sin(angle), 0, np.cos(angle)]
])
def make_rotation_matz(angle):
return np.float32([
[np.cos(angle), -np.sin(angle), 0],
[np.sin(angle), np.cos(angle), 0],
[0, 0, 1]
])
def compute_rotate(face_norm):
# find rx and ry (rz=0) to rotate (0,0,1) to face_norm
rx = np.arcsin(-face_norm[1])
cos_rx = np.cos(rx)
sin_ry = face_norm[0]/(cos_rx+1e-4)
cos_ry = face_norm[2]/(cos_rx+1e-4)
if sin_ry>1:
sin_ry=1
elif sin_ry<-1:
sin_ry=-1
if cos_ry>1:
cos_ry=1
elif cos_ry<-1:
cos_ry=-1
ry = np.arcsin(sin_ry)
if cos_ry>0 and (ry<-np.pi/2 or ry>np.pi/2):
ry = np.pi - ry
elif cos_ry<0 and (ry>-np.pi/2 and ry<np.pi/2):
ry = np.pi - ry
rt = np.matmul(make_rotation_matx(-rx), make_rotation_maty(-ry))
r = np.linalg.inv(rt)
return rt, r
def make_rodrigue_rotation_mat(vect, alpha):
cos_a = np.cos(alpha)
sin_a = np.sin(alpha)
wx, wy, wz = vect
return np.float32([
[cos_a+wx**2*(1-cos_a), wx*wy*(1-cos_a)-wz*sin_a, wy*sin_a+wx*wz*(1-cos_a)],
[wz*sin_a+wx*wy*(1-cos_a), cos_a+wy**2*(1-cos_a), -wx*sin_a+wy*wz*(1-cos_a)],
[-wy*sin_a+wx*wz*(1-cos_a), wx*sin_a+wy*wz*(1-cos_a), cos_a+wz**2*(1-cos_a)]])
def compute_css_rotate(face_points, face_norm):
cos_rx = face_norm[2]/ np.sqrt(face_norm[1]**2+face_norm[2]**2 + 1e-8)
sin_rx = -face_norm[1]/ np.sqrt(face_norm[1]**2+face_norm[2]**2 + 1e-8)
rx = np.arcsin(sin_rx)
if cos_rx>0 and (rx<-np.pi/2 or rx>np.pi/2):
rx = np.pi - rx
elif cos_rx<0 and (rx>-np.pi/2 and rx<np.pi/2):
rx = np.pi - rx
cos_ry = np.sqrt(face_norm[1]**2 + face_norm[2]**2)
sin_ry = face_norm[0]
ry = np.arcsin(sin_ry)
if cos_ry>0 and (ry<-np.pi/2 or ry>np.pi/2):
ry = np.pi - ry
elif cos_ry<0 and (ry>-np.pi/2 and ry<np.pi/2):
ry = np.pi - ry
mat_rx = make_rodrigue_rotation_mat([1, 0, 0], rx)
mat_ry = make_rodrigue_rotation_mat([0, np.cos(rx), np.sin(rx)], ry)
mat_r_xy = np.matmul(mat_ry, mat_rx)
rt, r = compute_rotate(face_norm)
ori_points = np.matmul(rt, face_points.T)
dz = np.mean(ori_points[2])
bounds = ori_points.T[:,:2]
mat_rz = np.matmul(r, np.linalg.inv(mat_r_xy)) # mat_rz
wx, wy, wz = face_norm
try:
a = np.float32([[wz, -wx*wy],[-wy, -wx*wz]])
b = np.float32([mat_rz[1,0]-wx*wy, mat_rz[2,0]-wx*wz])
temp_sin_rz, temp_cos_rz = np.linalg.solve(a, b)
sin_rz = temp_sin_rz/np.sqrt(temp_sin_rz**2 + temp_cos_rz**2)
cos_rz = temp_cos_rz/np.sqrt(temp_sin_rz**2 + temp_cos_rz**2)
rz = np.arcsin(sin_rz)
if cos_rz>0 and (rz<-np.pi/2 or rz>np.pi/2):
rz = np.pi - rz
elif cos_rz<0 and (rz>-np.pi/2 and rz<np.pi/2):
rz = np.pi - rz
except:
rz = 0
mat_rz = make_rodrigue_rotation_mat(face_norm, rz)
r_css = np.matmul(mat_rz, mat_r_xy)
return {
"transform_mat": r_css,
"bounds": bounds,
"z": dz,
"rotation":{
"x": rx,
"y": ry,
"z": rz
}
}
def write_files(objects, file_name):
VIEW_SIZE = 360
css_text = '.model3d_' + file_name.lower() + '_model_container {\n'
css_text += '\twidth: ' + str('{:.2f}'.format(VIEW_SIZE)) + 'px;\n'
css_text += '\theight: ' + str('{:.2f}'.format(VIEW_SIZE)) + 'px;\n'
css_text += '\tperspective: 10000px;\n'
css_text += '\ttransform-style: preserve-3d;\n'
css_text += '\tperspective-origin: 50% 50%;\n'
css_text += '\tdisplay: flex;\n'
css_text += '\tjustify-content: center;\n'
css_text += '\talign-items: center;\n'
css_text += '\ttransform-origin: 50% 50%;\n'
css_text += '\tanimation: rotate360 10s infinite linear;\n'
css_text += '}\n'
css_text += '.model3d_' + file_name.lower() + '_model_face {\n'
css_text += '\tposition: absolute;\n'
css_text += '\ttop: 50%;\n'
css_text += '\tleft: 50%;\n'
css_text += '}\n'
css_text += '@keyframes rotate360 {\n'
css_text += '\tfrom {\n'
css_text += '\t\ttransform: translateY(-20px) rotateX(-10deg) rotateY(0deg);\n'
css_text += '\t}\n'
css_text += '\tto {\n'
css_text += '\t\ttransform: translateY(-20px) rotateX(-10deg) rotateY(360deg);\n'
css_text += '\t}\n'
css_text += '}\n'
html_text = '<html>\n'
html_text += '\t<head>\n'
html_text += '\t\t<link rel="stylesheet" href="./' + file_name + '.css">\n'
html_text += '\t</head>\n'
html_text += '\t<body>\n'
html_text += '\t\t<div class="model3d_' + file_name.lower() + '_model_container">\n'
for object_name in objects.keys():
object = objects[object_name]
count = 0
color = np.float32([int(object_name[1:3], 16), int(object_name[3:5], 16), int(object_name[5:7], 16)])
for plane in object:
norm = plane['norm']
face = plane['face']
para = compute_css_rotate(face, norm)
classname = 'model3d_' + file_name.lower() + '_model_' + object_name[1:].lower() + '_face' + str(count)
count += 1
html_text += '\t\t\t<div class="model3d_' + file_name.lower() + '_model_face ' + classname + '"></div>\n'
css_text += '.' + classname + ' {\n'
color_shade = (np.sum(np.float32([-1,-1,1])*norm)/np.sqrt(3) + 1) / 2
color_shade = 0.6 + 0.35*color_shade
r,g,b = color * color_shade
css_text += '\tbackground-color: rgb(' + str('{:.2f}'.format(r)) + ',' +str('{:.2f}'.format(g)) + ',' +str('{:.2f}'.format(b)) + ');\n'
min_x = np.min(para["bounds"][:,0])
max_x = np.max(para["bounds"][:,0])
min_y = np.min(para["bounds"][:,1])
max_y = np.max(para["bounds"][:,1])
center_x = (max_x + min_x)/2
center_y = (max_y + min_y)/2
ori_center = np.matmul(para["transform_mat"], [[center_x], [center_y], [para["z"]]])
ori_center = np.reshape(ori_center, [3]) * VIEW_SIZE/2
xs = (para["bounds"][:,0] - min_x) * (VIEW_SIZE/2)
ys = (para["bounds"][:,1] - min_y) * (VIEW_SIZE/2)
width = (max_x-min_x)*VIEW_SIZE/2
height = (max_y-min_y)*VIEW_SIZE/2
css_text += '\twidth: ' + str('{:.2f}'.format(width)) + 'px;\n'
css_text += '\theight: ' + str('{:.2f}'.format(height)) + 'px;\n'
bounds = list(zip(xs,ys))
bounds = [str('{:.2f}'.format(point[0]))+'px ' + str('{:.2f}'.format(point[1]))+'px' for point in bounds]
bounds = 'polygon(' + (', '.join(bounds)) + ')'
css_text += '\tclip-path: ' + bounds + ';\n'
transition = 'translateX(' + str('{:.2f}'.format(ori_center[0] - width/2)) + 'px) translateY('+ str('{:.2f}'.format(ori_center[1] - height/2)) + 'px) translateZ(' + str('{:.2f}'.format(ori_center[2])) + 'px)'
rx, ry, rz = para["rotation"]["x"], para["rotation"]["y"], para["rotation"]["z"]
rx = rx / np.pi * 180
ry = ry / np.pi*180
rz = rz / np.pi*180
rotation = 'rotateX(' + str('{:.2f}'.format(rx)) + 'deg) rotateY(' + str('{:.2f}'.format(ry)) + 'deg) rotateZ(' + str('{:.2f}'.format(rz)) + 'deg)'
css_text += '\ttransform: ' + transition + ' ' + rotation + '\n'
css_text += '}\n'
html_text += '\t\t</div>\n'
html_text += '\t</body>\n'
html_text += '</html>\n'
html_file = open(file_name + ".html", "w")
html_file.write(html_text)
html_file.close()
css_file = open(file_name + ".css", "w")
css_file.write(css_text)
css_file.close()
name = sys.argv[1]
objs = load_data(name + '.obj')
write_files(objs, name)3 . CSS変換処理
3.1. まずBlenderソフトで3Dモデルを作成します。
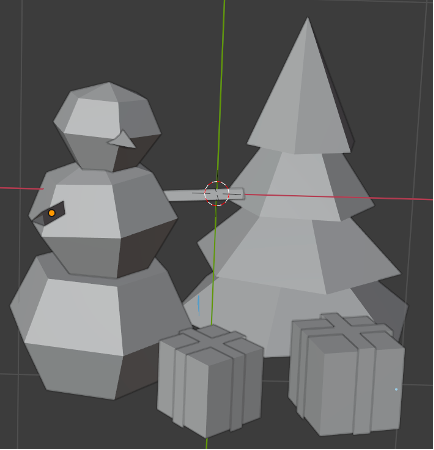
注意:できるだけ、オブジェクトのポイントの範囲は[-1,-1,-1] から[1, 1, 1]までにした方が表示しやすいです。
3.2. 同じ色の部分を1オブジェクトをまとめ、オブジェクト名を色コードにします。
例:木の色を緑にする場合は、木のオブジェクト名を「#32a852」にします。
3.3. モデルを三角形に分割するため、モデルを*.OBJファイルとしてExportします。Exportされるファイルにある全平面は全て三角形になります。
※今回Exportするファイル名は「Christmax.obj」とします。
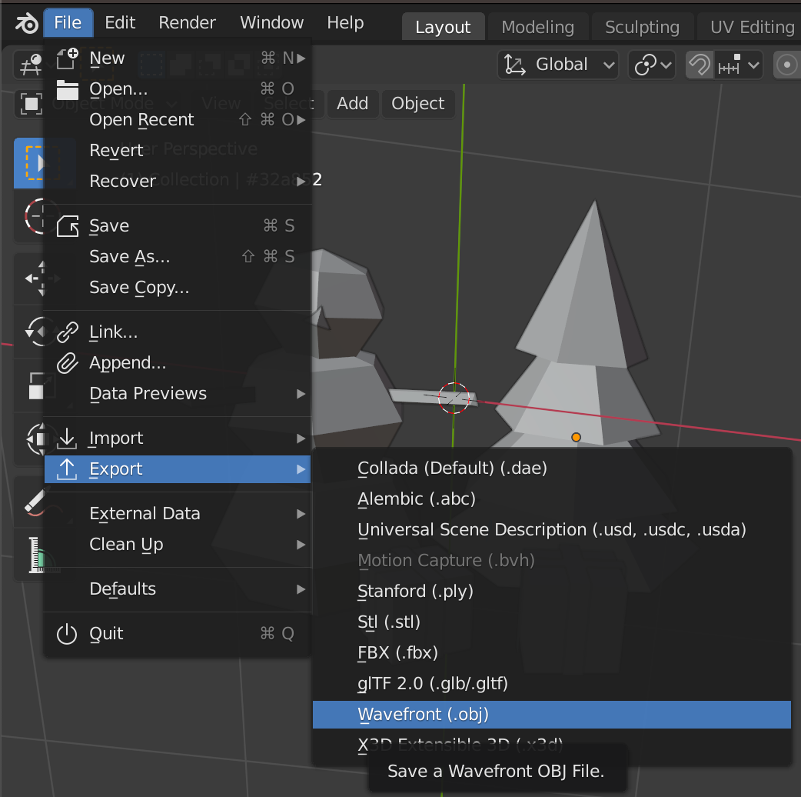
3.4. 出力された*.OBJファイルを2.7のconvert.pyソースコードファイルと同じフォルダーに移動し、以下のコマンドを実行します。
python3 convert.py Christmax- convert.py :PYTHONソースコードファイル名。
- Christmax : *.OBJファイル名、拡張子「.obj」を無視する。
3.5. ソースコードを実行完了してから、「Christmax.html」と「Christmax.css」が出力されます。
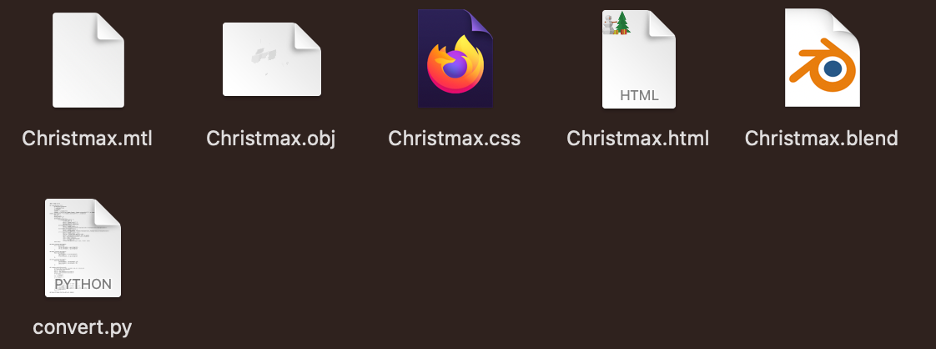
HTMLファイルを実行するとブラウザが起動し、以下のアニメーションが表示されます。